Варианты программы, полученые путем переупорядочивания предложений и целей
Уже в примерах программ гл. 1 существовала скрытая опасность зацикливания. Определение отношения предок в этой главе было таким:
предок( X, Z) :-
родитель( X, Z).
предок( X, Z) :-
родитель( X, Y),
предок( Y, Z).
Проанализируем некоторые варианты этой программы. Ясно, что все варианты будут иметь одинаковую декларативную семантику, но разные процедурные семантики.
В соответствии с декларативной семантикой Пролога мы можем, не меняя декларативного смысла, изменить
(1) порядок предложений в программе и
(2) порядок целей в телах предложений.
Процедура предок состоит из двух предложений, и одно из них содержит в своем теле две цели. Возможны, поэтому, четыре варианта данной программы, все с одинаковым декларативным смыслом. Эти четыре варианта можно получить, если
(1) поменять местами оба предложения и
(2) поменять местами цели в каждом из этих двух последовательностей предложений.
Соответствующие процедуры, названные пред1, пред2, пред3 и пред4, показаны на рис. 2.16.
Есть существенная разница в поведении этих четырех декларативно эквивалентных процедур. Чтобы это продемонстрировать, будем считать, отношение родитель определенным так, как показано на рис. 1.1 гл. 1. и посмотрим, что произойдет, если мы спросим, является ли Том предком Пат, используя все четыре варианта отношения предок:
?- пред1( том, пат).
да
?- пред2( том, пат).
да
?- пред3( том, пат).
да
?- пред4( том, пат).
line();
% Четыре версии программы предок
% Исходная версия
пред1( X, Z) :-
родитель( X, Z).
пред1( X, Z) :-
родитель( X, Y),
пред1( Y, Z).
% Вариант а: изменение порядка предложений в исходной версии
пред2( X, Z) :-
родитель( X, Y),
пред2( Y, Z).
пред2( X, Z) :-
родитель( X, Z).
% Вариант b: изменение порядка целей во втором предложении
% исходной версии
пред3( X, Z) :-
родитель( X, Z).
пред3( X, Z) :-
пред3( X, Y),
родитель( Y, Z).
% Вариант с: изменение порядка предложений и целей в исходной
% версии
пред4( X, Z) :-
пред4( X, Y),
родитель( Y, Z).
пред4( X, Z):-
родитель( X, Z).
line();
Рис. 2. 16. Четыре версии программы предок.
В последнем случае пролог-система не сможет найти ответа. И выведет на терминал сообщение: "Не хватает памяти".
На рис. 1.11 гл. 1 были показаны все шаги вычислений по пред1 (в главе 1 она называлась предок), предпринятые для ответа на этот вопрос. На рис 2.17 показаны соответствующие вычисления по пред2, пред3
и пред4. На рис. 2.17 (с) ясно видно, что работа пред4 - бесперспективна, а рис. 2.17(а) показывает, что пред2 довольно неэффективна по сравнению с пред1: пред2
производит значительно больший перебор и делает больше возвратов по фамильному дереву.
Такое сравнение должно напомнить нам об общем практическом правиле при решении задач: обычно бывает полезным прежде всего попробовать самое простое соображение.
В нашем случае все версии отношения предок основаны на двух соображениях:
- более простое - нужно проверить, не удовлетворяют ли два аргумента отношения предок отношению родитель;
- более сложное - найти кого-либо "между" этими двумя людьми (кого-либо, кто связан с ними отношениями родитель и предок).
Наши четыре варианта процедуры предок можно далее сравнить, рассмотрев вопрос: "На какие типы вопросов может отвечать тот или иной конкретный вариант и на какие не может?" Оказывается, пред1 и пред2 оба способны найти ответ на любой вид вопроса относительно предков; пред4 никогда не находит ответа, а пред3 иногда может найти, иногда нет. Вот пример вопроса, на который пред4 ответить не может:
?- пред3( лиз, джим).
Такой вопрос тоже вводит систему в бесконечную рекурсию. Следовательно и пред3 нельзя признать верным с точки зрения процедурного смысла.
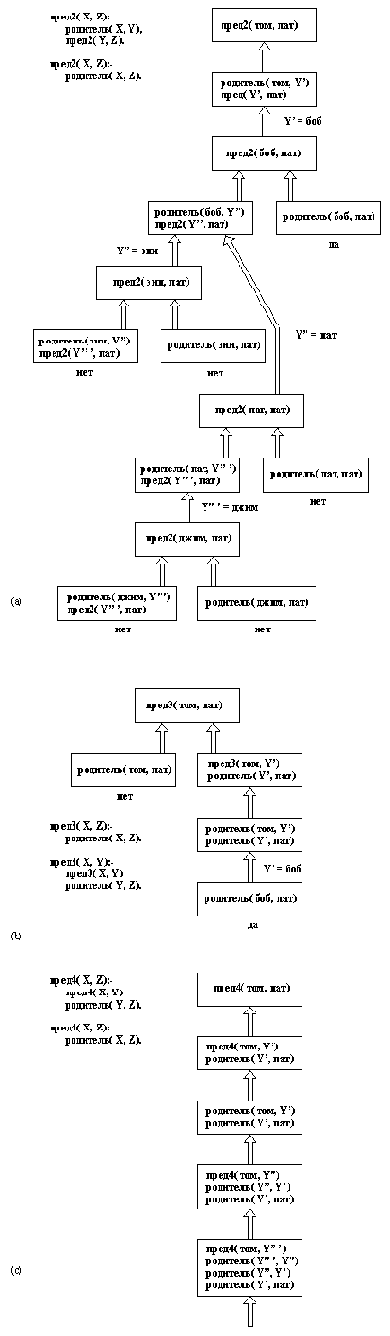
Рис. 2. 17. Поведение трех вариантов формулировки отношения
предок при ответе на вопрос, является ли Том предком Пат?