Структуры
Структурные объекты (или просто структуры) - это объекты, которые состоят из нескольких компонент. Эти компоненты, в свою очередь, могут быть структурами. Например, дату можно рассматривать как структуру, состоящую из трех компонент: день, месяц, год. Хотя они и составлены из нескольких компонент, структуры в программе ведут себя как единые объекты. Для того, чтобы объединить компоненты в структуру, требуется выбрать функтор. Для нашего примера подойдет функтор дата. Тогда дату 1-е мая 1983 г. можно записать так:
дата( 1, май, 1983)
(см. рис. 2.2).
Все компоненты в данном примере являются константами (две компоненты - целые числа и одна - атом). Компоненты могут быть также переменными или структурами. Произвольный день в мае можно представить структурой:
дата( День, май, 1983)
Заметим, что День является переменной и ей можно приписать произвольное значение на некотором более позднем этапе вычислений.
Такой метод структурирования данных прост и эффективен. Это является одной из причин того, почему Пролог естественно использовать для решения задач обработки символьной информации.
Синтаксически все объекты данных в Прологе представляют собой термы. Например,
май
и
дата( 1, май, 1983)
суть термы.
Все структурные объекты можно изображать в виде деревьев (пример см. на рис. 2.2). Корнем дерева служит функтор, ветвями, выходящими из него, - компоненты. Если некоторая компонента тоже является структурой, тогда ей соответствует поддерево в дереве, изображающем весь структурный объект.
Наш следующий пример показывает, как можно использовать структуры для представления геометрических объектов (см. рис. 2.3). Точка в двумерном пространстве определяется двумя координатами; отрезок определяется двумя точками, а треугольник можно задать тремя точками. Введем следующие функторы:
точка
для точек
отрезок
для отрезков и
треугольник
для треугольников.
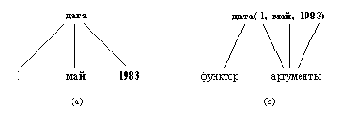
Рис. 2. 2. Дата - пример структурного объекта:
(а) его представление в виде дерева; (б) запись на Прологе.
Тогда объекты, приведенные на рис. 2.3, можно представить следующими прологовскими термами:
Р1 = точка( 1, 1)
P2 = точка( 2, 3)
S = отрезок( P1, P2) =
отрезок( точка( 1, 1), точка( 2, 3) )
Т = треугольник( точка( 4, 2), точка( 6, 4),
точка( 7, 1) )
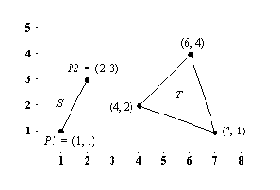
Рис. 2. 3. Простые геометрические объекты.
Соответствующее представление этих объектов в виде деревьев приводится на рис. 2.4. Функтор, служащий
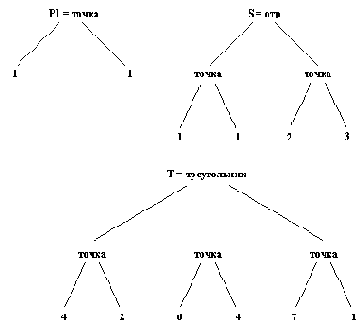
Рис. 2. 4. Представление объектов с рис. 2.3 в виде деревьев.
корнем дерева, называется главным функтором терма.
Если бы в такой же программе фигурировали точки трехмерного пространства, то можно было бы для их представления использовать другой функтор, скажем точка3:
точка3( X, Y, Z)
Можно, однако, воспользоваться одним и тем же именем точка одновременно и для точек двумерного и трехмерного пространств и написать, например, так:
точка( XI, Y1) и точка ( X, Y, Z)
Если одно и то же имя появляется в программе в двух различных смыслах, как в вышеупомянутом примере с точкой, то пролог-система будет различать их по числу аргументов и интерпретировать это имя как два функтора: один - двухаргументный; второй - трех. Это возможно потому, что каждый функтор определяется двумя параметрами:
(1) именем, синтаксис которого совпадает с синтаксисом атомов;
(2) арностью - т. е. числом аргументов.
Как уже объяснялось, все структурные объекты в Прологе - это деревья, представленные в программе термами. Рассмотрим еще два примера, чтобы показать, насколько удобно сложные объекты данных представляются с помощью прологовских термов. На рис. 2.5 показана древовидная структура, соответствующая арифметическому выражению
(а + в)*(с - 5)
В соответствии с введенным к настоящему моменту синтаксисом, такое выражение, используя символы *, + и - в качестве функторов, можно записать следующим образом:
*( +( а, в), -( с, 5) )
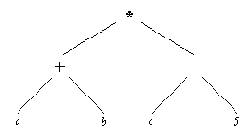
Рис. 2. 5. Древовидная структура, соответствующая арифметическому
выражению (а + w)*(s - 5).
Это, конечно, совершенно правильный прологовский терм, однако это не та форма, которую нам хотелось бы иметь, при записи арифметических выражений. Хотелось бы применять обычную инфиксную запись, принятую в математике. На самом деле Пролог допускает использование инфиксной нотации, при которой символы *, + и - записываются как инфиксные операторы. Детали того, как программист может определять свои собственные операторы, мы приведем в гл. 3.
В качестве последнего примера рассмотрим некоторые простые электрические цепи, изображенные на рис. 2.6. В правой части рисунка помещены древовидные представления этих цепей. Атомы r1, r2, r3 и r4 - имена резисторов. Функторы пар и посл обозначают соответственно параллельное и последовательное соединение резисторов.Вот соответствующие прологовские термы:
посл( r1, r2)
пар( r1, r2)
паp( rl, пap( r2, r3) )
пар( r1, посл( пар( r2, r3), r4) )
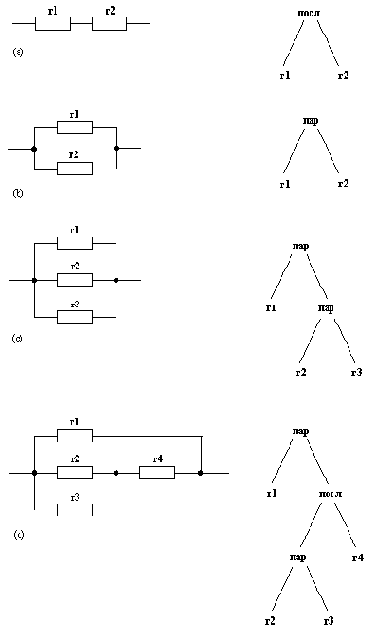
Рис. 2. 6. Некоторые простые электрические цепи и их представление: (а) последовательное соединение резисторов rl и r2; (b) параллельное соединение двух резисторов; (с) параллельное соединение трех резисторов; (d) параллельное соединение r1 и еще одной цепи.