Поиск с предпочтением
Программу поиска с предпочтением можно получить как результат усовершенствования программы поиска в ширину (рис. 11.13). Подобно поиску в ширину, поиск с предпочтением начинается со стартовой вершины и использует множество путей-кандидатов. В то время, как поиск в ширину всегда выбирает для продолжения самый короткий путь (т.е. переходит в вершины наименьшей глубины), поиск с предпочтением вносит в этот принцип следующее усовершенствование: для каждого кандидата вычисляется оценка и для продолжения выбирается кандидат с наилучшей оценкой.
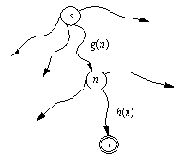
Рис. 12. 1. Построение эвристической оценки f(n) стоимости
самого дешевого пути из s в t, проходящего через n: f(n) = g(n) + h(n).
Мы будем в дальнейшем предполагать, что для дуг пространства состояний определена функция стоимости с(n, n') - стоимость перехода из вершины n к вершине-преемнику n'.
Пусть f - это эвристическая оценочная функция, при помощи которой мы получаем для каждой вершины n оценку f( n) "трудности" этой вершины. Тогда наиболее перспективной вершиной-кандидатом следует считать вершину, для которой f принимает минимальное значение. Мы будем использовать здесь функцию f специального вида, приводящую к хорошо известному А*-алгоритму. Функция f( n) будет построена таким образом, чтобы давать оценку стоимости оптимального решающего пути из стартовой вершины s к одной из целевых вершин при условии, что этот путь проходит через вершину n. Давайте предположим, что такой путь существует и что t - это целевая вершина, для которой этот путь минимален. Тогда оценку f( n) можно представить в виде суммы из двух слагаемых (рис. 12.1):
f( n) = g( n) + h( n)
Здесь g( n) - оценка оптимального пути из s в n; h( n) - оценка оптимального пути из n в t.
Когда в процессе поиска мы попадаем в вершину n, мы оказываемся в следующей ситуация: путь из s в n уже найден, и его стоимость может быть вычислена как сумма стоимостей составляющих его дуг. Этот путь не обязательно оптимален (возможно, существует более дешевый, еще не найденный путь из s в n), однако стоимость этого пути можно использовать в качестве оценки g(n) минимальной стоимости пути из s в n. Что же касается второго слагаемого h(n), то о нем трудно что-либо сказать, поскольку к этому моменту область пространства состояний, лежащая между n и t, еще не "изучена" программой поиска. Поэтому, как правило, о значении h(n) можно только строить догадки на основании эвристических соображений, т.е. на основании тех знаний о конкретной задаче, которыми обладает алгоритм. Поскольку значение h зависит от предметной области, универсального метода для его вычисления не существует. Конкретные примеры того, как строят эти "эвристические догадки", мы приведем позже. Сейчас же будем считать, что тем или иным способом функция h задана, и сосредоточим свое внимание на деталях нашей программы поиска с предпочтением.
Можно представлять себе поиск с предпочтением следующим образом. Процесс поиска состоит из некоторого числа конкурирующих между собой подпроцессов, каждый из которых занимается своей альтерна-
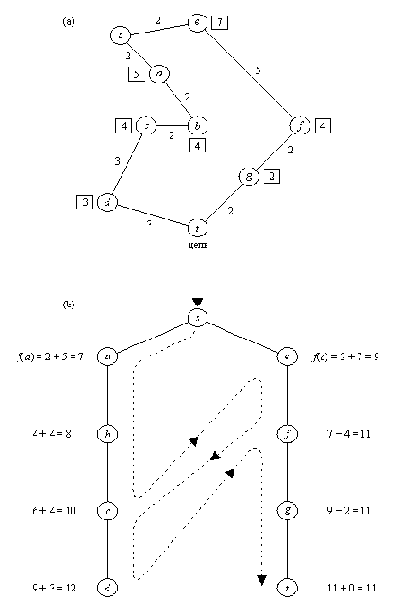
Рис. 12. 2. Поиск кратчайшего маршрута из s в t. (а) Карта со
связями между городами; связи помечены своими длинами; в
квадратиках указаны расстояния по прямой до цели t.
(b) Порядок, в котором при поиске с предпочтением происходит
обход городов. Эвристические оценки основаны на расстояниях
по прямой. Пунктирной линией показано переключение активности
между альтернативными путями. Эта линия задает тот порядок, в
котором вершины принимаются для продолжения пути, а не тот
порядок, в котором они порождаются.
тивой, т.е. просматривает свое поддерево. У поддеревьев есть свои поддеревья, их просматривают подпроцессы подпроцессов и т.д. В каждый данный момент среди всех конкурирующих процессов активен только один - тот, который занимается наиболее перспективной к настоящему моменту альтернативой, т.е. альтернативой с наименьшим значением f. Остальные процессы спокойно ждут того момента, когда f-оценки изменятся и в результате какая-нибудь другая альтернатива станет наиболее перспективной. Тогда производится переключение активности на эту альтернативу. Механизм активации-дезактивации процессов функционирует следующим образом: процесс, работающий над текущей альтернативой высшего приоритета, получает некоторый "бюджет" и остается активным до тех пор, пока его бюджет не исчерпается. Находясь в активном состоянии, процесс продолжает углублять свое поддерево. Встретив целевую вершину, он выдает соответствующее решение. Величина бюджета, предоставляемого процессу на данный конкретный запуск, определяется эвристической оценкой конкурирующей альтернативы, ближайшей к данной.
На рис. 12.2 показан пример поведения конкурирующих процессов. Дана карта, задача состоит в том, чтобы найти кратчайший маршрут из стартового города s в целевой город t. В качестве оценки стоимости остатка маршрута из города Х до цели мы будем использовать расстояние по прямой расст( X, t) от Х до t. Таким образом,
f( Х) = g( X) + h( X) = g( X) + расст( X, t)
Мы можем считать, что в данном примере процесс поиска с предпочтением состоит из двух процессов. Каждый процесс прокладывает свой путь - один из двух альтернативных путей: Процесс 1 проходит через а. Процесс 2 - через е. Вначале Процесс 1 более активен, поскольку значения f вдоль выбранного им пути меньше, чем вдоль второго пути. Когда Процесс 1 достигает города с, а Процесс 2 все еще находится в е, ситуация меняется:
f( с) = g( c) + h( c) = 6 + 4 = 10
f( e) = g( e) + h( e) = 2 + 7 = 9
Поскольку f( e) < f( c), Процесс 2 переходит к f, a Процесс 1 ждет. Однако
f( f) = 7 + 4 = 11
f( c) = 10
f( c) < f( f)
Поэтому Процесс 2 останавливается, а Процессу 1 дается разрешение продолжать движение, но только до d, так как f( d) = 12 > 11. Происходит активация Процесса 2, после чего он, уже не прерываясь, доходит до цели t.
Мы реализуем этот механизм программно при помощи усовершенствования программы поиска в ширину (рис. 11.13). Множество путей-кандидатов представим деревом. Дерево будет изображаться в программе в виде терма, имеющего одну из двух форм:
(1) л( В, F/G) - дерево, состоящее из одной вершины (листа); В - вершина пространства состояний, G - g( B) (стоимость уже найденного пути из стартовой вершины в В); F - f( В) = G + h( В).
(2) д( В, F/G, Пд) - дерево с непустыми поддеревьями; В - корень дерева, Пд - список поддеревьев; G - g( B); F - уточненное значение f( В), т.е. значение f для наиболее перспективного преемника вершины В; список Пд упорядочен в порядке возрастания f-оценок поддеревьев.
Уточнение значения f необходимо для того, чтобы дать программе возможность распознавать наиболее перспективное поддерево (т.е. поддерево, содержащее наиболее перспективную концевую вершину) на любом уровне дерева поиска. Эта модификация f-оценок на самом деле приводит к обобщению, расширяющему область определения функции f. Теперь функция f определена не только на вершинах, но и на деревьях.
Для одновершинных деревьев (листов) n остается первоначальное определение
f( n) = g( n) + h( n)
Для дерева T с корнем n, имеющем преемников m1, m2, ..., получаем
f( T) = min f( mi )
i
Программа поиска с предпочтением, составленная в соответствии с приведенными выше общими соображениями, показана на рис 12.3. Ниже даются некоторые дополнительные пояснения.
Так же, как и в случае поиска в ширину (рис. 11.13), ключевую роль играет процедура расширить, имеющая на этот раз шесть аргументов:
расширить( Путь, Дер, Предел, Дер1, ЕстьРеш, Решение)
Эта процедура расширяет текущее (под)дерево, пока f-оценка остается равной либо меньшей, чем Предел.
line(); % Поиск с предпочтением
эврпоиск( Старт, Решение):-
макс_f( Fмакс). % Fмакс > любой f-оценки
расширить( [ ], л( Старт, 0/0), Fмакс, _, да, Решение).
расширить( П, л( В, _ ), _, _, да, [В | П] ) :-
цель( В).
расширить( П, л( В, F/G), Предел, Дер1, ЕстьРеш, Реш) :-
F <= Предел,
( bagof( B1/C, ( после( В, В1, С), not принадлежит( В1, П)),
Преемники), !,
преемспис( G, Преемники, ДД),
опт_f( ДД, F1),
расширить( П, д( В, F1/G, ДД), Предел, Дер1,
ЕстьРеш, Реш);
ЕстьРеш = никогда). % Нет преемников - тупик
расширить( П, д( В, F/G, [Д | ДД]), Предел, Дер1,
ЕстьРеш, Реш):-
F <= Предел,
опт_f( ДД, OF), мин( Предел, OF, Предел1),
расширить( [В | П], Д, Предел1, Д1, ЕстьРеш1, Реш),
продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,
ЕстьРеш1, ЕстьРеш, Реш).
расширить( _, д( _, _, [ ]), _, _, никогда, _ ) :- !.
% Тупиковое дерево - нет решений
расширить( _, Дер, Предел, Дер, нет, _ ) :-
f( Дер, F), F > Предел. % Рост остановлен
продолжить( _, _, _, _, да, да, Реш).
продолжить( П, д( В, F/G, [Д1, ДД]), Предел, Дер1,
ЕстьРеш1, ЕстьРеш, Реш):-
( ЕстьРеш1 = нет, встав( Д1, ДД, НДД);
ЕстьРеш1 = никогда, НДД = ДД),
опт_f( НДД, F1),
расширить( П, д( В, F1/G, НДД), Предел, Дер1,
ЕстьРеш, Реш).
преемспис( _, [ ], [ ]).
преемспис( G0, [В/С | ВВ], ДД) :-
G is G0 + С,
h( В, Н), % Эвристика h(B)
F is G + Н,
преемспис( G0, ВВ, ДД1),
встав( л( В, F/G), ДД1, ДД).
% Вставление дерева Д в список деревьев ДД с сохранением
% упорядоченности по f-оценкам
встав( Д, ДД, [Д | ДД] ) :-
f( Д, F), опт_f( ДД, F1),
F =< F1, !.
встав( Д, [Д1 | ДД], [Д1 | ДД1] ) ) :-
встав( Д, ДД, ДД1).
% Получение f-оценки
f( л( _, F/_ ), F). % f-оценка листа
f( д( _, F/_, _ ) F). % f-оценка дерева
опт_f( [Д | _ ], F) :- % Наилучшая f-оценка для
f( Д, F). % списка деревьев
опт_f( [ ], Fмакс) :- % Нет деревьев:
мaкс_f( Fмакс). % плохая f-оценка
мин( X, Y, X) :-
Х =< Y, !.
мин( X, Y, Y).
line(); Рис. 12. 3. Программа поиска с предпочтением.
Аргументы процедуры расширить имеют следующий смысл:
Путь Путь между стартовой вершиной и корнем дерева Дер.
Дер Текущее (под)дерево поиска.
Предел Предельное значение f-оценки, при котором допускается расширение.
Дер1 Дерево Дер, расширенное в пределах ограничения Предел;
f-оценка дерева Дер1 больше, чем Предел ( если только при расширении не была обнаружена целевая вершина).
ЕстьРеш Индикатор, принимающий значения "да", "нет" и "никогда".
Решение Решающий путь, ведущий из стартовой вершины через дерево Дер1
к целевой вершине и имеющий стоимость, не превосходящую ограничение Предел (если такая целевая вершина была обнаружена).
Переменные Путь, Дер, и Предел - это "входные" параметры процедуры расширить в том смысле, что при каждом обращении к расширить они всегда конкретизированы. Процедура расширить порождает результаты трех видов. Какой вид результата получен, можно определить по значению индикатора ЕстьРеш следующим образом:
(1) ЕстьРеш = да.
Решение = решающий путь, найденный при расширении дерева Дер с учетом ограничения Предел.
Дер1 = неконкретизировано.
(2) ЕстьРеш = нет
Дер1 = дерево Дер, расширенное до тех пор, пока его f-оценка не превзойдет Предел (см. рис. 12.4).
Решение = неконкретизировано.
(3) ЕстьРеш = никогда.
Дер1 и Решение = неконкретизированы.
В последнем случае Дер является "тупиковой" альтернативой, и соответствующий процесс никогда не будет реактивирован для продолжения просмотра этого дерева. Случай этот возникает тогда, когда f-оценка дерева Дер не превосходит ограничения Предел, однако дерево не может "расти" потому, что ни один его лист не имеет преемников, или же любой преемник порождает цикл.
Некоторые предложения процедуры расширить требуют пояснений. Предложение, относящееся к наиболее сложному случаю, когда Дер имеет поддеревья, т.е.
Дер = д( В, F/G, [Д | ДД ] )
означает следующее. Во-первых, расширению подвергается наиболее перспективное дерево Д. В качестве ограничения этому дереву выдается не Предел, а не-

Рис. 12. 4. Отношение расширить: расширение дерева Дер до тех
пор, пока f-оценка не превзойдет Предел, приводит к дереву Дер1.
которое, возможно, меньшее значение Предел1, зависящее от f-оценок других конкурирующих поддеревьев ДД. Тем самым гарантируется, что "растущее" дерево - это всегда наиболее перспективное дерево, а переключение активности между поддеревьями происходит в соответствии с их f-оценками. После того, как самый перспективный кандидат расширен, вспомогательная процедура продолжить решает, что делать дальше, а это зависит от типа результата, полученного после расширения. Если найдено решение, то оно и выдается, в противном случае процесс расширения деревьев продолжается.
Предложение, относящееся к случаю
Дер = л( В, F/G)
порождает всех преемников вершины В вместе со стоимостями дуг, ведущих в них из В. Процедура преемспис формирует список поддеревьев, соответствующих вершинам-преемникам, а также вычисляет их g- и f-оценки, как показано на рис. 12.5. Затем полученное таким образом дерево подвергается расширению с учетом ограничения Предел. Если преемников нет, то переменной ЕстьРеш придается значение "никогда" и в результате лист В покидается навсегда.
Другие отношения:
после( В, В1, С) В1 - преемник вершины В; С - стоимость дуги, ведущей из В в В1.
h( В, Н) Н - эвристическая оценка стоимости оптимального пути
из вершины В в целевую вершину.
макс_f( Fмакс) Fмакс - некоторое значение, задаваемое пользователем,
про которое известно, что оно больше любой возможной f-оценки.
В следующих разделах мы покажем на примерах, как можно применить нашу программу поиска с предпочтением к конкретным задачам. А сейчас сделаем несколько заключительных замечаний общего характера относительно этой программы. Мы реализовали один из вариантов эвристического алгоритма, известного в литературе как А*-алгоритм (ссылки на литературу см. в конце главы). А*-алгоритм привлек внимание многих исследователей. Здесь мы приведем один важный результат, полученный в результате математического анализа А*-алгоритма:
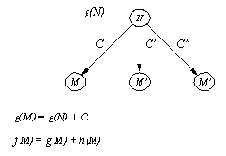
Рис. 12. 5. Связь между g-оценкой вершины В и f- и g-оценками
ее "детей" в пространстве состояний.
line(); Алгоритм поиска пути называют допустимым, если он всегда отыскивает оптимальное решение (т.е. путь минимальной стоимости) при условии, что такой путь существует. Наша реализация алгоритма поиска, пользуясь механизмом возвратов, выдает все существующие решения, поэтому, в нашем случае, условием допустимости следует считать оптимальность первого из найденных решений. Обозначим через h*(n) стоимость оптимального пути из произвольной вершины n в целевую вершину. Верна следующая теорема о допустимости А*-алгоритма: А*-алгоритм, использующий эвристическую функцию h, является допустимым, если
h( n) <= h*( n)
для всех вершин n пространства состояний.
line(); Этот результат имеет огромное практическое значение. Даже если нам не известно точное значение h*, нам достаточно найти какую-либо нижнюю грань h* и использовать ее в качестве h в А*-алгоритме - оптимальность решения будет гарантирована.
Существует тривиальная нижняя грань, а именно:
h( n) = 0, для всех вершин n пространства состояний.
И при таком значении h допустимость гарантирована.Однако такая оценка не имеет никакой эвристической силы и ничем не помогает поиску. А*-алгоритм при h=0 ведет себя аналогично поиску в ширину. Он, действительно, превращается в поиск в ширину, если, кроме того, положить с(n, n' )=1 для всех дуг (n, n') пространства состояний. Отсутствие эвристической силы оценки приводит к большой комбинаторной сложности алгоритма. Поэтому хотелось бы иметь такую оценку h, которая была бы нижней гранью h* (чтобы обеспечить допустимость) и, кроме того, была бы как можно ближе к h* (чтобы обеспечить эффективность). В идеальном случае, если бы нам была известна сама точная оценка h*, мы бы ее и использовали: А*-алгоритм, пользующийся h*, находит оптимальное решение сразу, без единого возврата.