Перестановки
Иногда бывает полезно построить все перестановки некоторого заданного списка. Для этого мы определим отношение перестановка с двумя аргументами. Аргументы - это два списка, один из которых является перестановкой другого. Мы намереваемся порождать перестановки списка с помощью механизма автоматического перебора, используя процедуру перестановка, подобно тому, как это делается в следующем примере:
?- перестановка( [а, b, с], Р).
Р = [а, b, с];
Р = [а, с, b];
Р = [b, а, с];
. . .
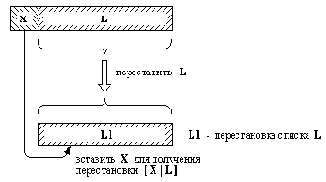
Рис. 3. 5. Один из способов построения перестановки списка [X | L].
Программа для отношения перестановка в свою очередь опять может основываться на рассмотрении двух случаев в зависимости от вида первого списка:
(1) Если первый список пуст, то и второй список должен быть пустым.
(2) Если первый список не пуст, тогда он имеет вид [Х | L], и перестановку такого списка можно построить так, как Это показано на рис. 3.5: вначале получить список L1 - перестановку L, а затем внести Х в произвольную позицию L1.
Два прологовских предложения, соответствующих этим двум случаям, таковы:
перестановка( [ ], [ ]).
перестановка( [X | L ], Р) :-
перестановка( L, L1),
внести( X, L1, Р).
Другой вариант этой программы мог бы предусматривать удаление элемента Х из первого списка, перестановку оставшейся его части - получение списка Р, а затем добавление Х в начало списка Р. Соответствующая программа такова:
перестановка2( [ ], [ ]).
перестановка2( L, [X | Р] ) :-
удалить( X, L, L1),
перестановка2( L1, Р).
Поучительно проделать несколько экспериментов с нашей программой перестановки. Ее нормальное использование могло бы быть примерно таким:
?- перестановка( [красный, голубой, зеленый], Р).
Как и предполагалось, будут построены все шесть перестановок:
Р = [ красный, голубой, зеленый];
Р = [ красный, зеленый, голубой];
Р = [ голубой, красный, зеленый];
Р = [ голубой, зеленый, красный];
Р = [ зеленый, красный, голубой];
Р = [ зеленый, голубой, красный];
nо (нет)
Приведем другой вариант использования процедуры перестановка:
?- перестановка( L, [а, b, с] ).
Наша первая версия, перестановка, произведет успешную конкретизацию L всеми шестью перестановками. Если пользователь потребует новых решений, он никогда не получит ответ "нет", поскольку программа войдет в бесконечный цикл, пытаясь отыскать новые несуществующие перестановки. Вторая версия, перестановка2, в этой ситуации найдет только первую (идентичную) перестановку, а затем сразу зациклится. Следовательно, при использовании этих отношений требуется соблюдать осторожность.