Двоичные справочники: добавление и удаление элемента
Если мы имеем дело с динамически изменяемым множеством элементов данных, то нам может понадобиться внести в него новый элемент или удалить из него один из старых. В связи с этим набор основных операций, выполняемых над множеством S, таков:
внутри( X, S) % Х содержится в S
добавить( S, X, S1) % Добавить Х к S, результат - S1
удалить( S, X, S1) % Удалить Х из S, результат - S1
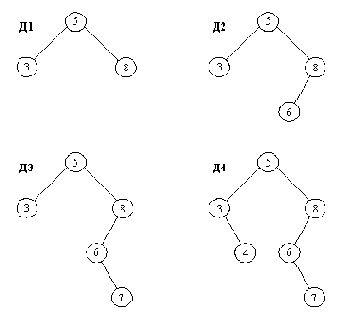
Рис. 9. 9. Введение в двоичный справочник нового элемента на уровне листьев. Показанные деревья соответствуют следующей последовательности вставок:
добавить( Д1, 6, Д2), добавить( Д2, 6, Д3), добавить( Д3, 6, Д4)
доблист( nil, X, дер( nil, X, nil) ).
доблист( дер( Лев, Х, Прав), Х, дер( Лев, Х, Прав) ).
доблист( дер( Лев, Кор, Прав), Х, дер( Лев1, Кор, Прав)) :-
больше( Кор, X),
доблист( Лев, X, Лев1)).
доблист( дер( Лев, Кор, Прав), Х, дер( Лев, Кор, Прав1)) :-
больше( X, Кор),
доблист( Прав, X, Прав1).
Рис. 9. 10. Вставление в двоичный справочник нового элемента в качестве листа.
Определим отношение добавить. Простейший способ: ввести новый элемент на самый нижний уровень дерева, так что он станет его листом. Место, на которое помещается новый элемент, выбрать таким образом, чтобы не нарушить упорядоченность дерева. На рис. 9.9 показано, какие изменения претерпевает дерево в процессе введения в него новых элементов. Назовем такой метод вставления элемента в множество
доблист( Д, X, Д1)
Правила добавления элемента на уровне листьев таковы:
- Результат добавления элемента Х к пустому дереву есть дерево дер( nil, X, nil).
- Если Х совпадает с корнем дерева Д, то Д1 = Д (в множестве не допускается дублирования элементов).
- Если корень дерева Д больше, чем X, то Х вносится в левое поддерево дерева Д; если корень меньше, чем X, то Х вносится в правое поддерево.
Теперь рассмотрим операцию удалить. Лист дерева удалить легко, однако удалить какую-либо внутреннюю вершину - дело не простое. Удаление листа можно на самом деле определить как операцию, обратную
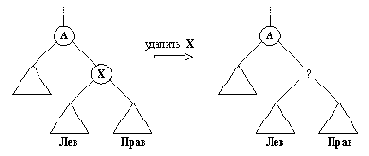
Рис. 9. 11. Удаление X из двоичного справочника. Возникает проблема наложения "заплаты" на место удаленного элемента X.
операции добавления листа:
удлист( Д1, X, Д2) :-
доблист( Д2, X, Д1).
К сожалению, если Х - это внутренняя вершина, то такой способ не работает, поскольку возникает проблема, иллюстрацией к которой служит рис. 9.11. Вершина Х имеет два поддерева Лев и Прав. После удаления вершины Х в дереве образуется "дыра", и поддеревья Лев и Прав теряют свою связь с остальной частью дерева. К вершине А оба эти поддерева присоединить невозможно, так как вершина А способна принять только одно из них.
Если одно из поддеревьев Лев и Прав пусто, то существует простое решение: подсоединить к А непустое поддерево. Если же оба поддерева непусты,
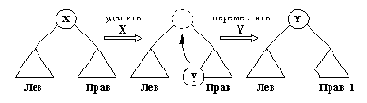
Рис. 9. 12. Заполнение пустого места после удаления X.
то можно использовать следующую идею (рис. 9.12): если самую левую вершину Y поддерева Прав переместить из ее текущего положения вверх и заполнить ею пробел, оставшийся после X, то упорядоченность дерева не нарушится. Разумеется, та же идея сработает и в симметричном случае, когда перемещается самая правая вершина поддерева Лев.
На рис. 9.13 показана программа, реализующая операцию удаления элементов в соответствии с изложенными выше соображениями. Основную работу по перемещению самой левой вершины выполняет отношение
удмин( Дер, Y, Дер1)
Здесь Y - минимальная (т.е. самая левая) вершина дерева Дер, а Дер1 - то, во что превращается дерево Дер после удаления вершины Y.
Существует другой, элегантный способ реализация операции добавить и удалить. Отношение добавить можно сделать недетерминированным в том смысле, что новый элемент вводится на произвольный уровень дерева, а не только на уровень листьев. Правила таковы:
line(); уд( дер( nil, X, Прав), X, Прав).
уд( дер( Лев, X, nil), X, Лев).
уд( дер( Лев, Х, Прав), X, дер( Лев,Y, Прав1) ) :-
удмин( Прав, Y, Прав1).
уд( дер( Лев, Кор, Прав), X, дер( Лев1, Кор, Прав) ) :-
больше( Кор, X),
уд( Лев, X, Лев1).
уд( дер( Лев, Кор, Прав), X, дер( Лев, Кор, Прав1) ) :-
больше( X, Кор),
уд( Прав, X, Прав1).
удмин( дер( nil, Y, Прав), Y, Прав).
удмин( дер( Лев, Кор, Прав), Y, дер( Лев1, Кор, Прав) ) :-
удмин( Лев, Y, Лев1).
line(); Рис. 9. 13. Удаление элемента из двоичного справочника.
line(); Для того, чтобы добавить Х в двоичный справочник Д, необходимо одно из двух:
- добавить Х на место корня дерева (так, что Х станет новым корнем) или
- если корень больше, чем X, то внести Х в левое поддерево, иначе - в правое поддерево.
добкор( Д, X, X1)
где Х - новый элемент, вставляемый вместо корня в Д, а Д1 - новый справочник с корнем Х. На рис. 9.14 показано, как соотносятся X, Д и Д1. Остается вопрос: что из себя представляют поддеревья L1 и L2 (или, соответственно, R1 и R2) на рис. 9.14?
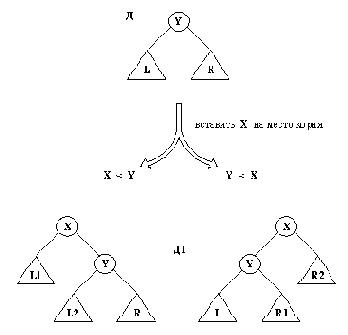
Рис. 9. 14. Внесение Х в двоичный справочник в качестве корня.
Ответ мы получим, если учтем следующие ограничения на L1, L2:
- L1 и L2 - двоичные справочники;
- множество всех вершин, содержащихся как в L1, так и в L2, совпадает с множеством вершин справочника L;
- все вершины из L1 меньше, чем X; все вершены из L2 больше, чем X.
добкор( L, X, дер( L1, X, L2) ).
Те же самые ограничения применимы к R1, R2:
добкор( R, X, дер( R1, X, R2) ).
line(); добавить( Д, X, Д1) :- % Добавить Х на место корня
добкор( Д, X, Д1).
добавить( дер( L, Y, R), X, дер( L1, Y, R) ) :-
больше( Y, X), % Ввести Х в левое поддерево
добавить( L, X, L1).
добавить( дер( L, Y, R), X, дер( L, Y, R1) ) :-
больше( X, Y), % Ввести Х в правое поддерево
добавить( R, X, R1).
добкор( nil, X, дер( nil, X, nil) ). % Ввести Х в пустое дерево
добкор( дер( L, Y, R), Х, дер( L1, Х, дер( L2, Y, R) )) :-
больше( Y, X),
добкор( L, X, дер( L1, X, L2) ).
добкор( дep( L, Y, R), X, дep( дep( L, Y, R1), X, R2) ) :-
больше( X, Y),
добкор( R, X, дер( R1, X, R2) ).
line(); Рис. 9. 15. Внесение элемента на произвольный уровень двоичного справочника.
На рис. 9.15 показана программа для "недетерминированного" добавления элемента в двоичный справочник.
Эта процедура обладает тем замечательным свойством, что в нее не заложено никаких ограничений на уровень дерева, в который вносится новый элемент. В связи с этим операцию добавить можно использовать "в обратном направлении" для удаления элемента из справочника. Например, приведенная ниже последовательность целей строит справочник Д, содержащий элементы 3, 5, 1, 6, а затем удаляет из него элемент 5, после чего получается справочник ДД:
добавить( nil, 3, Д1), добавить( Д1, 5, Д2),
добавить( Д2, 1, Д3), добавить( Д3, 6, Д),
добавить( ДД, 5, Д).
Назад | Содержание | Вперёд